三点共线与三线共点的证明方法

一、三点共线的常用证明方法
(一)利用平角180°
例1 如图,点d是等腰直角三角形abc内一点.将△adc绕点c顺时针旋转90°得到△bec,点d的对应点为点e.
(1)如果ad:cd:bd=1:2:3,求证:a,d,e三点共线;
(2)如果a,d,e三点共线,ad,cd,bd满足什么样的关系?
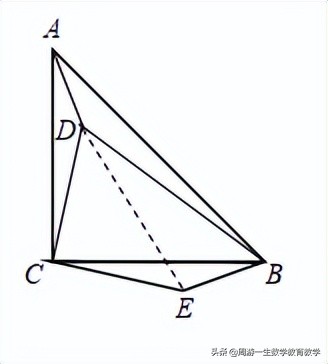
解析:(1)连接de,欲证a、d、e三点共线,只需要证明∠ade=180°,即证∠adc ∠cde=180°.
由旋转,可知:cd=ce,∠dce=90°,ad=be,∠adc=bec,
所以△cde是等腰直角三角形,
所以∠cde=∠ced=45°,
因为ad:cd:bd=1:2:3,
所以可设ad=be=a,cd=2a,bd=3a,
则de=2√2a,
所以be2 de2=a2 8a2=9a2=bd2,
所以∠bed=90°,
所以∠ceb=135°=∠adc,
所以∠ade=135° 45°=180°,
所以a、d、e三点共线;
(2)逆着(1)的思路可知:如果a,d,e三点共线,ad,cd,bd满足的关系是:ad2 2cd2=bd2.
(二)利用平行公理
例2 如图,等边△abc中,d为ab边上一点(点d不与点a、b重合),连接cd,将cd平移到be(其中点b和c对应),将△bcd绕着点b逆时针旋转至△baf,求证:d、f、e三点共线.
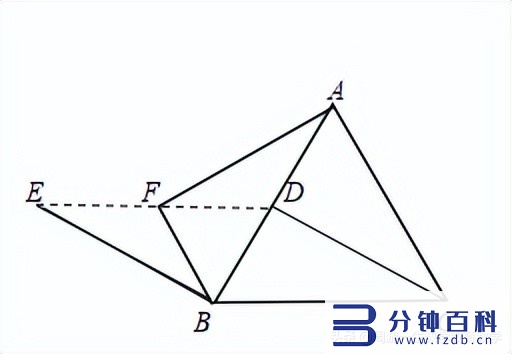
解析:连接de,df,欲证d、f、e三点共线,只需要证明de,df平行于同一条直线即可.
由平移可得:be平行且等于cd,
所以四边形bcde是平行四边形,
所以de//bc;
由旋转,得:bf=bd,∠dbf=∠dbc=60°,
所以△bdf是等边三角形,
所以∠bdf=60°=∠dbc,
所以df//bc,
由平行公理可知de、df是同一条直线,
所以d、f、e三点共线.
二、三线共点的常用证明方法
(一)转化为三点共线的证明
例3 如图,菱形abcd中,∠b=60°,p是bc延长线上一点,连接ap.点m是线段ap上的点,满足∠amc=120°,求证:直线ab,cm,pd相交于同一点.
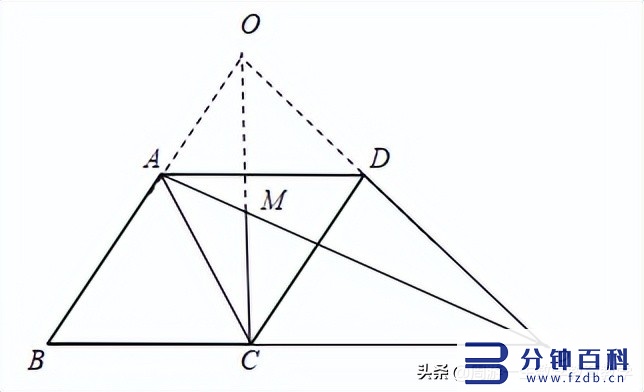
解析:首先设ab、cm相交于点o,连接od,则欲证直线ab,cm,pd相交于同一点,只需要证明o、d、p三点共线即可.
因为四边形abcd是菱形,∠b=60°,
所以△abc和△acd都是等边三角形,
所以∠cad=60°,
即∠cam ∠mad=60°,
因为∠amc=120°,
所以∠cao ∠aco=60°,
所以∠mad=∠aco,
又因为ad//bp,
所以∠mad=∠apc,
所以∠aco=∠apc,
又∠oac=∠acp=120°,
所以△aco∽△cpa,
所以ac:cp=ao:ac,
因为ac=cd=ad,
所以cd:cp=ao:ad,
因为∠oad=∠dcp=60°,
所以△oad∽△dcp,
所以∠oda=∠dpc,
所以∠odp=∠oda ∠adc ∠cdp
=∠dpc ∠dcp ∠cdp
=180°,
所以o、d、p三点共线,
所以直线ab,cm,pd相交于同一点o.
(二)利用同一法则
例4 如图,矩形abcd中,e是bc上的动点,延长eb到f,使bf=be,g为ad的中点,求证:直线ae,bg,df三线共点.
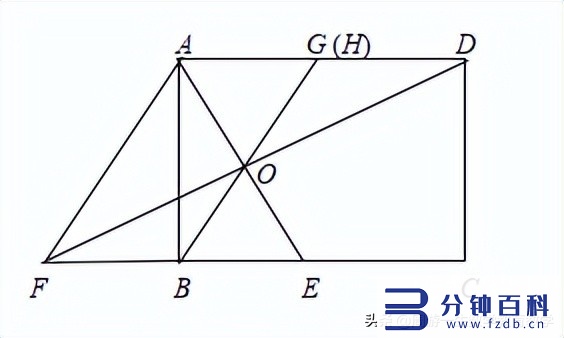
解析:设ae、df相交于点o,连接bo并延长交ad于h,则欲证直线ae,bg,df三线共点,只需要证明bg和bh是同一条直线,即证点h是ad的中点即可.
因为ad//bc,
所以△oah∽△obe,
所以ah:be=oh:ob,
同理,dh:bf=oh:ob,
所以ah:be=dh:bf,
因为be=bf,所以ah=dh,
所以h是ad的中点,
因为g是ad的中点,
所以bh和bg是同一条直线,
所以直线ae,bg,df三线共点.